Technical Debt is Entropy In Software
Entropy #
Entropy is the ultimate boss battle [1]. As the reason why ice melts, why tires burst, and why ink diffuses – thermodynamic entropy is a fact of the physical world, sharply following the arrow of time [2].
The Second Law of Thermodynamics states
For an isolated system, entropy will either increase or remain the same over time; decreases require exporting entropy to the environment.
There’s something about inevitability that I think is fascinating, especially when you can see it unfold in front of you – my favourite visualisation is below (thanks Gemini).

This picture displays the three stages of entropy:
- Infancy: when the ink enters the water
- Expansion: when the ink diffuses through water
- Maturity: when the ink and water have fully merged
So, how does entropy grow? Academics and practitioners alike believe that entropy follows an S-curve [4], with its three stages likened to those of ink diffusing in water.
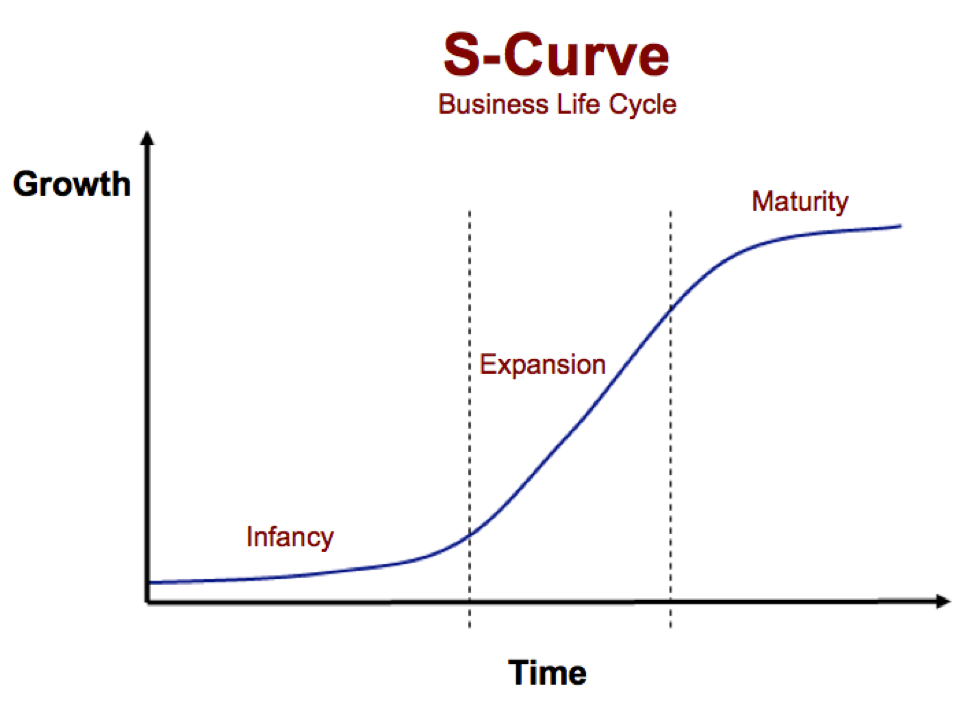
This is strikingly similar to the business lifecycle curve above! Indeed, prior art agrees that business and technology lifecycles are overlaid entropy curves [5].
Entropy in business is largely a representation of diffusion of a particular product, driven by the forces of supply and demand. While entropy is often likened to “disorder”, I like to use “disruption” - permeation of new (ink) into old (water). It is neither good nor bad, simply inevitable.
Properties of Entropy #
Statistical Entropy #
Since we are talking about software and not atoms, let’s turn to information theory to understand the information contained in software programs.
In information theory, Shannon’s entropy is, for a random variable \( X \) distributed according to \( p: (x \in \mathcal{X}) \rightarrow [0, 1] \):
$$ H(X) = - \sum_{x \in \mathcal{X}} p(x)\log(p(x)) $$
While this may look obscure at first, the formulation begets two properties:
Property 1. The number of possible states that a system can have is generally proportional to the total entropy in a system. A dice with 6 sides has more entropy than one with 4 sides.
Property 2. Higher entropy is correlated with a higher presence of tail events. Gaussians and exponentials are maximum entropy distributions (under certain statistical conditions [3]), but they are light-tailed. Many real-world systems are heavier-tailed (Taleb-style), so tail risk is larger than Gaussian intuition suggests [16].
Complexity #
Complexity is entropy’s first cousin. Formally we’ll use Kolmogorov complexity:
\(K(o)\) for an object \(o\) is the length of the shortest program that produces the object as output.
In other words, it measures how “compressible” something is.
Now - how does entropy relate to complexity? Modis posits the following relation [4][15]:
Complexity is the time derivative of entropy. Given that entropy is an S-curve, complexity is roughly normally distributed.
With time, complexity increases until a peak and decreases after.
To see this: let’s consider Scott Aaronson’s lucid example around cream dissolving into coffee [6].
His research empirically calculated a complexity score using the gzip compression
file size of pictures of cream melting in the coffee.
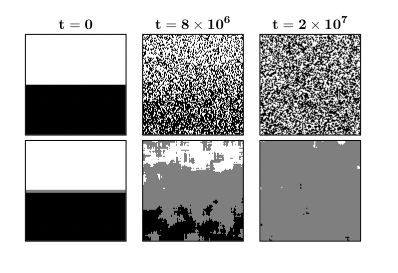
The picture above represents snapshots of the coffee cup at the three phases of entropy. As the cream and coffee begin to mix, complexity increases until a maximum before decreasing as the mixture becomes saturated and homogeneous.
It is simple to see why the first and last image can be more easily compressed (i.e are less complex) compared to the image in the middle.
Where Does Software Fit Into This? #
Let’s start by quantifying where software is today in its business lifecycle / entropy curve.
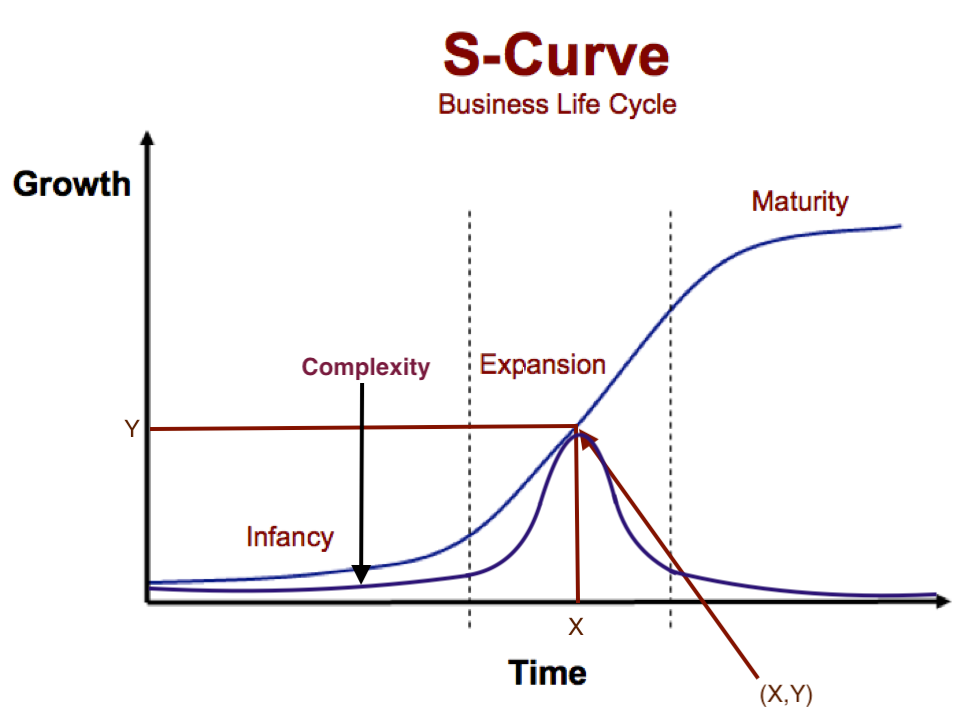
As in the graph above, I think we are around (X,Y) today.
Why?
Software is still custom-made / productised. SaaS “exploded” but hasn’t permeated all industries. Digital modernisation efforts continue to be in higher demand than available supply, indicating superlinear business growth or relative convexity – we are close to the central inflection point.
Software complexity is close to peaking. For starters, the cloud has driven the successful commoditisation of infrastructure. We now have the ability to run software cheaply and easily.
What’s left is to reduce the complexity of the specification of software (language and layers of abstraction) that runs on said infrastructure. Prediction: LLMs are statistical program compression tools [12] and will do exactly this.
Tech Debt as Complexity #
For a particular business, technological modernisation is largely bottlenecked by iteration speed to a desired solution. I view tech debt as the maintenance and complexity related resistance to change that causes this bottleneck.
To be clear, every problem that software solves has some theoretical baseline level of “complexity” needed to meet its specification. Technical debt is simply the add-on difference in complexity between the ideal and real world solutions.
So what causes complexity? The sources of complexity that I’ve found to be the most concise yet accurate are below [7]:
Complexity via obscurity #
Poorly designed software abstractions (obscurity) generate more complexity - “garbage in, garbage out”.
The core issue with “obscure” abstractions is that they are uncompressed representations of state. Their interfaces are inherently complex, where they should instead be simple and hide deep complexity [11].
Often times, obscurity appears due to constraints imposed on systems (“make this code accept XYZ data format”). Local optimisations lead to global API changes that introduce obscurity and state bloat [17]. Refactors / complexity regulation measures don’t fit into deadlines and this bloat almost always compounds (Property 1).
Complexity via dense dependency graphs #
Software that depends on A LOT of other software is more prone to bugs, vulnerabilities and maintenance overhead. This kind of technical debt introduces some obscurity but also “tail-risk” around software (Property 2).
The number of failures due to weaknesses
in the open source parts of a software supply chain increased by 650% between
2020 and 2021 [8]. At the same time, OSS adoption has been growing 70% YoY [9], bringing with it
increasingly public vulnerabilities like in log4j, xz, OpenSSH etc.
Dependencies can also reflect a level of “obscurity” in software that may not justify their added risk. Leftpad is a great example here! [18]
What isn’t captured by mere probabilities is how this “tail-risk” can manifest as devastatingly high-impact Black Swan events [14]: massive cybercrimes affecting data protection and financial security. Software outage affecting the global economy. We’ve all seen them play out.
Conclusion #
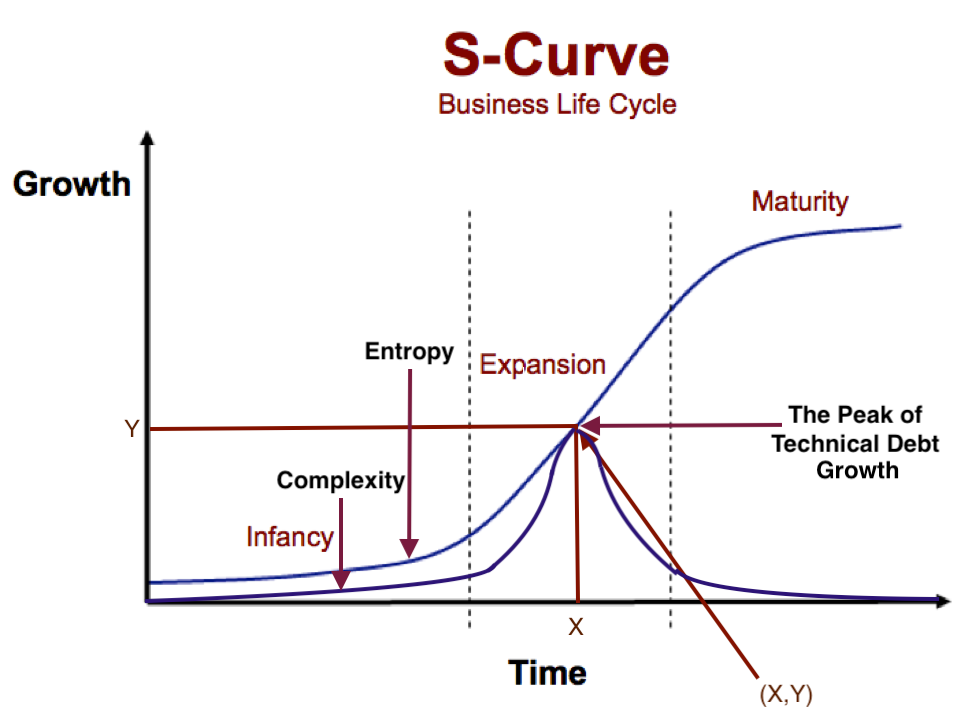
To recap, entropy in software tracks the expansion of software with time and complexity is the derivative of entropy. Due to the S-curve shape of entropy and thus “normal” shape of its derivative, “complexity begets complexity” until a certain point in time, after which complexity reduces.
I argue that due to market conditions: namely the state of SaaS as a product / custom-made offering and the commoditisation of infrastructure (cloud) that we are at the middle of the S-curve. i.e., we are at the peak of software complexity / tech debt growth. Intuitively, in the business “experimental -> custom -> product -> commodity” lifecycle, software is at the custom/product intersection, which is somewhere in the middle.
While the total amount of code in the world will keep growing, in order to sustain healthy growth, demand for “software regulators” will rise to address growing maintenance and lifecycle management costs. In order to get from product to commodity and therefore fully permeate society, operating software needs to be far simpler and cheaper.
Economically, McKinsey estimates that tech debt accounts for 40% of IT balance sheets and up to 50% of developer time [13]. It shows up as a vicious cycle that organisations increasingly have a harder time escaping from (remember: complexity begets complexity).

A report on software quality in 2022 attaches a $2.4 trillion price tag to technical debt in the form of poor quality and overly complex software [8]. However, if you interchange loosely with “technological opportunity cost”, the real business value is of course far higher:
The total technological debt includes entirely “untapped” digital transformation in industries (??T) + the canonical “poorly tapped” form of tech debt (2.4T).
A lot of words to say: there’s a whole lot left to do here.
Footnotes and References #
[1] https://x.com/elonmusk/status/1090689205586472960
[2] https://en.wikipedia.org/wiki/Entropy_as_an_arrow_of_time
[3] https://pillowlab.princeton.edu/teaching/statneuro2018/slides/notes08_infotheory.pdf
[4] https://arxiv.org/abs/2410.10844
[5] http://www.growth-dynamics.com/articles/Forecasting_Complexity.pdf
[6] https://arxiv.org/abs/1405.6903
[8] https://www.it-cisq.org/wp-content/uploads/sites/6/2022/11/CPSQ-Report-Nov-22-2.pdf
[9] https://www.sonatype.com/blog/the-scale-of-open-source-growth-challenges-and-key-insights
[10] https://en.wikipedia.org/wiki/Lindy_effect
[11] https://en.wikipedia.org/wiki/Everything_is_a_file
[12] https://arxiv.org/abs/2309.10668
[14] https://en.wikipedia.org/wiki/Black_swan_theory
[15] Theodore Modis presents an excellent information-theoretic analysis of the relation between complexity and entropy: his claim held true over a 20 year prediction (2002-2022) [4] (a Lindy trend [10]).
[16] https://arxiv.org/pdf/1412.7647
[17] https://www.hillelwayne.com/post/complexity-constraints/
[18] https://en.wikipedia.org/wiki/Npm_left-pad_incident
Appendix: Three Hard Problems #
I’ve spent a lot of words talking about a problem and tying it to theory and predictions. What does taming complexity look like? How do we roll the ball down the peak of the hill?
At the risk of being tongue-in-cheek, I’ll start by saying I think the solution will involve solving the “three hardest problems” in computer science.
Naming #
Naming standards solve the literal naming problem. Today, standards work - they just suffer from enforcement and distribution problems. Because of this, the shapes of software abstractions haven’t been globally standardised. It’s a problem famous enough to warrant its own obligatory XKCD.
Because of where we are on the software S-curve, I suspect the move from product to commodity will entail hiding the naming problem with higher-order abstractions. As people move up an abstraction layer, user-defined names will simply matter less.
Caching #
What’s hard about caching isn’t maintaining caching infrastructure, but rather defining the correct cache key and invalidation policy. This isn’t impossible - it again just requires precise and well-defined behaviour. The CPU caches are a great success story here - they just needed maturity in the CPU/memory interface.
- With cacheability, you get reproducibility, determinism, and more general fungibility of building blocks. With fungibility of building blocks - you get commodity-like properties!
- Declarative specifications of components are closely tied to cacheability - a statement which traces the entire history of software infrastructure growth and commoditisation (Kubernetes, Docker, Terraform, Nix, Bazel etc).
Off by one errors #
These simply represent human hallucinations. Execution driven feedback. i.e unit test cases encapsulating abstractions “solve” this well.
Prove it? #
I won’t elaborate too much on “solutions” since I have various hypotheses-in-testing that need iteration (as opposed to more ideation).
If you made it this far, clearly some of this was interesting to you. Let’s chat! Email X